Linii Importante în Triunghi


1. MEDIATOAREA ÎN TRIUNGHI

Se numește mediatoarea unui segment dreapta perpendiculară pe mijlocul segmentului.

Teoremă: Dacă un punct este situat pe mediatoarea unui segment, atunci acel punct este egal departat de capetele segmentului.
 
Teoremă: Mediatoarele unui triunghi sunt concurente într-un punct numit centrul cercului circumscris triunghiului.

ATENȚIE! Centrul cercului circumscris triunghiului este la egală depărtare față de vârfurile triunghiului.


2. BISECTOAREA  ÎN  TRIUNGHI

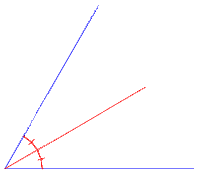
Se numește bisectoarea unui unghi semidreapta aflată în interiorul unghiului, cu originea în vârful unghiului, care împarte unghiul în două unghiuri congruente.

Teoremă: Dacă un punct este situat pe bisectoarea unui unghi, atunci acel punct este egal departat de laturile triunghiului.


Teoremă: Bisectoarele tuturor unghiurilor unui triunghi sunt concurente într-un punct numit centrul cercului înscris în triunghi.

3. ÎNĂLȚIMEA ÎN TRIUNGHI

Se numește înălțimea unui triunghi segmentul dus din vârful unui triunghi pe latura opusă.

Teoremă: Înălțimile unui triunghi sunt concurente într-un punct numit ortocentru  ( H ).




4. MEDIANA  ÎN  TRIUNGHI

Se numește mediană în triunghi segmentul determinat de un vârf și mijlocul laturii opuse.



Teoremă: Medianele unui triunghi sunt concurente într-un punct numit centrul de greutate ( G ).

ATENȚIE! Centrul de greutate se află la doua treimi de vârf (2/3) și o treime de bază (1/3).



Teoremă: Într-un triunghi dreptunghic mediana corespunzatoare ipotenuzei are ca valoare jumatate din lungimea ipotenuzei.

5. LINIA MIJLOCIE ÎN TRIUNGHI

Se numește linie mijlocie în triunghi segmentul determinat de mijloacele a două laturi ale triunghiului.

Teoremă: Într-un triunghi linia mijlocie este paralelă cu o latura a triunghiului și are lungimea egală cu jumatate din lungimea laturii cu care ea este paralelă.


Comentarii

Trimiteți un comentariu

Postări populare de pe acest blog

Exerciții cu Puteri și Calcule cu Paranteze

Imagine
1. Exersați proprietățile calculului cu puteri ( enumerate aici ): a) 2 5 b) 8 3 c) 15 2 d) 2017 0 e) 3 64 : 3 62 f) (4 2 ) 3 g) 1 2017   2. Efectuați: a)   2 30 : 2 26 - 2 - 2 10 : (4 2 ) 2 - 10 0 · 10 b)    [3 2 · 3 3 + 2 54 : 2 52 + (3 5 ) 4 : 3 20 ] : 31 c)    10 · [2 · 2 2 · 2 3 - 5 24 : 5 22 + (2 4 ) 5 : 2 19 ] d)   2 7 : 4 3 + 3 3 · 27 : 3 5 + (3 · 2 4 - 4 2 ) : 2 3 e)    (5 + 2 · 2 8 + 2 48 : 2 18 ) : [5 + 2 12 : 2 3 + (2 5 ) 6 ]   Rezolvarea Exercițiului 2: a)   2 30 : 2 26 - 2 - 2 10 : (4 2 ) 2 - 10 0 · 1 0 = = 2 30-26 - 2 - 2 10 : (2 2 ) 4 - 1 · 10 = = 2 4 - 2 - 2 10 : 2 8 - 10 =16-(2+2 2 +10) = 0 b)    [3 2 · 3 3 + 2 54 : 2 52 + (3 5 ) 4 : 3 20 ] : 31 = = (3 2+3 + 2 54-52 + 3 20 : 3 20 ) : 31 = = (3 5 + 2 2 + 1) : 31 = = (243 + 4 + 1) : 31 = = 248 : 31 = = 8 c)    10 · [2 · 2 2 · 2 3 - 5 24 : 5 22 + (2 4 ) 5 : 2 19 ] = = 10...
Citiți mai multe

Dreapta perpendiculara pe un plan

Imagine
Definitie:  O dreapta este perpendiculara pe un plan daca este perpendiculara pe orice dreapta din plan. Teorema:  O dreapta perpendiculara pe doua drepte concurente dintr-un plan este perpendiculara pe plan. Observatii: In aplicatii pentru a demonstra ca o dreapta este perpendiculara pe un plan folosim aceasta teorema. Pentru a arata ca doua drepte sunt perpendiculare, demonstram ca una din ele este perpendiculara pe un plan ce contine cealalta dreapta. Teorema:  Dintr-un punct se poate duce pe un plan o perpendiculara si numai una.(Analogie cu teorema: dintr-un punct exterior unei drepte se poate duce o perpendiculara pe acea dreapta si numai  una). Definitie:  Distanta dintre un punct si un plan este lungimea segmentului determinat de punct si de plan pe perpendiculara dusa din punct pe plan. Inaltimea piramidei Inaltimea piramidei este segmentul de pe perpendiculara dusa din varful piramidei pe baza. O piramida...
Citiți mai multe

Ridicarea la Putere a unui Număr Natural

Imagine
Definiție: Fie a și n două numere naturale. Numim puterea n a lui a produsul a n factori egali cu a notat a n .   a n = a · a· a· …………….· a  Citim a la puterea n . Numărul a se numește bază. Numărul n se numește exponent.   Așadar, ridicarea la putere este o înmulțire repetată. Baza ne arată ce număr se înmulțește cu el însuși, iar exponentul ne arată de câte ori. Exemple: a · a = a² a · a · a= a³  Excepții a 1   =  a    (Orice număr la puterea 1 este egal cu el însuși) a 0   =  1    (Orice număr la puterea 0 este egal cu 1) 1 n   =  1   (Unu ridicat la orice putere este tot 1) 0 n   =  0   (Zero ridicat la orice putere nenulă este zero, dar)   0 0 este operație fără sens, nu se calculează.   Reguli de calcul cu puteri:     Ridicarea la putere este o operație de ordinul III. Într-un exercițiu în c...
Citiți mai multe